Este post apresenta as notas de aula da semana 7 do curso online Probabilistic Graphical Models.

Estimativa de parâmetros em Redes Bayesianas
Estimativa de verossimilhança máxima
Dada uma amostra ![{\cal D} = \{x[1], \cdots, x[M] \}](https://s0.wp.com/latex.php?latex=%7B%5Ccal+D%7D+%3D+%5C%7Bx%5B1%5D%2C+%5Ccdots%2C+x%5BM%5D+%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) obtida de maneira independente de uma distribuição desconhecida, queremos estimar
obtida de maneira independente de uma distribuição desconhecida, queremos estimar 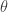 que represente
que represente  .
.
Uma medida da qualidade dessa distribuição é a verossimilhança, denotada por  e definida como a probabilidade de se obter
e definida como a probabilidade de se obter  dada a distribuição
dada a distribuição 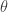 , ou seja
, ou seja
![L(\theta:{\cal D}) = P({\cal D}|\theta) = \prod_{i=1}^{M} P(x[i]|\theta)](https://s0.wp.com/latex.php?latex=L%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D+P%28%7B%5Ccal+D%7D%7C%5Ctheta%29+%3D+%5Cprod_%7Bi%3D1%7D%5E%7BM%7D+P%28x%5Bi%5D%7C%5Ctheta%29&bg=ffffff&fg=333333&s=0&c=20201002)
Definimos estatística suficiente como uma estatística que provê a mesma informação de uma amostra, sendo suficiente para calcularmos a verossimilhança. Vamos defini-la em termos de uma função que recebe uma amostra  e retorne uma tupla
e retorne uma tupla 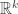 .
.
Um exemplo é a estatística suficiente para uma distribuição multinomial de 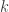 valores. Podemos definir a função
valores. Podemos definir a função  que recebe um valor
que recebe um valor  e retorna uma tupla apenas com a i-ésima posição contendo 1 e o resto 0.
e retorna uma tupla apenas com a i-ésima posição contendo 1 e o resto 0.
Agora calculamos a verossimilhança definindo ![\bar M = (M_1, \cdots, M_k) = \sum_{x[i] \in {\cal D}} s(x[i])](https://s0.wp.com/latex.php?latex=%5Cbar+M+%3D+%28M_1%2C+%5Ccdots%2C+M_k%29+%3D+%5Csum_%7Bx%5Bi%5D+%5Cin+%7B%5Ccal+D%7D%7D+s%28x%5Bi%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) . Note que
. Note que  representa o número de amostras com o valor
representa o número de amostras com o valor 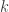 . Logo, a verossimilhança é dada por
. Logo, a verossimilhança é dada por

Outro exemplo é a distribuição Gaussiana com média 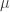 e variância
e variância 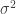 . A distribuição pode ser dada por
. A distribuição pode ser dada por

Podemos definir a estatística suficiente como 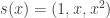 . Seja
. Seja
![\bar M = (M_1, M_2, M_3) = \sum_{x[i] \in {\cal D}} s(x[i])](https://s0.wp.com/latex.php?latex=%5Cbar+M+%3D+%28M_1%2C+M_2%2C+M_3%29+%3D+%5Csum_%7Bx%5Bi%5D+%5Cin+%7B%5Ccal+D%7D%7D+s%28x%5Bi%5D%29&bg=ffffff&fg=333333&s=0&c=20201002)
podemos escrever a função de verossimilhança como

O problema da estimativa de verossimilhança máxima (Maximum Likelihood Estimation, MLE) consiste em, dado um conjunto de amostras  , encontrar a distribuição
, encontrar a distribuição 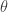 que maximiza a verossimilhança
que maximiza a verossimilhança  .
.
No caso da distribuição multinomial, podemos mostrar que o MLE é
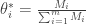
No caso da distribuição Gaussiana, temos
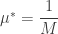
![\sigma^* = \sqrt{\dfrac{1}{M} \sum_m (x[m] - \mu^*)^2}](https://s0.wp.com/latex.php?latex=%5Csigma%5E%2A+%3D+%5Csqrt%7B%5Cdfrac%7B1%7D%7BM%7D+%5Csum_m+%28x%5Bm%5D+-+%5Cmu%5E%2A%29%5E2%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Estimativa de verossimilhança máxima em Redes Bayesianas
Podemos generalizar a estimativa de verossimilhança para as distribuições em Redes Bayesianas. Suponha que tenhamos uma rede Bayesiana e queremos estimar as distribuições de probabilidades, nesse caso, os CPDs.
Novamente, dado um conjunto de amostras,  , definimos a verossimilhança
, definimos a verossimilhança
![L(\Theta: D) = \prod_{m} P(x[m]:\Theta)](https://s0.wp.com/latex.php?latex=L%28%5CTheta%3A+D%29+%3D+%5Cprod_%7Bm%7D+P%28x%5Bm%5D%3A%5CTheta%29&bg=ffffff&fg=333333&s=0&c=20201002)
Podemos fatorar essa distribuição em um produto dos CPDs de cada nó 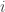 usando a regra da cadeia.
usando a regra da cadeia.
![= \prod_{m} \prod_i P(x_i[m] | \pmb{u}_i[m] : \theta_i)](https://s0.wp.com/latex.php?latex=%3D+%5Cprod_%7Bm%7D+%5Cprod_i+P%28x_i%5Bm%5D+%7C+%5Cpmb%7Bu%7D_i%5Bm%5D+%3A+%5Ctheta_i%29&bg=ffffff&fg=333333&s=0&c=20201002)
Neste caso  representa os pais da variável
representa os pais da variável 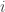 na rede. Re-arranjando os fatores, podemos trocar a ordem dos produtórios e obter,
na rede. Re-arranjando os fatores, podemos trocar a ordem dos produtórios e obter,
![= \prod_{i} \prod_m P(x_i[m] | \pmb{u}_i[m] : \theta_i)](https://s0.wp.com/latex.php?latex=%3D+%5Cprod_%7Bi%7D+%5Cprod_m+P%28x_i%5Bm%5D+%7C+%5Cpmb%7Bu%7D_i%5Bm%5D+%3A+%5Ctheta_i%29&bg=ffffff&fg=333333&s=0&c=20201002)
Definindo a verossimilhança local como
![L_i({\cal D}: \theta_i) = \prod_m P(x_i[m] | \pmb{u}_i[m] : \theta_i)](https://s0.wp.com/latex.php?latex=L_i%28%7B%5Ccal+D%7D%3A+%5Ctheta_i%29+%3D+%5Cprod_m+P%28x_i%5Bm%5D+%7C+%5Cpmb%7Bu%7D_i%5Bm%5D+%3A+%5Ctheta_i%29&bg=ffffff&fg=333333&s=0&c=20201002)
Temos finalmente que

Supondo inicialmente que os CPDs não são compartilhados por nenhuma variável, temos um 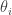 para cada variável. Vamos mostrar como determinar esses CPDs de maneira independente.
para cada variável. Vamos mostrar como determinar esses CPDs de maneira independente.
![L_i({\cal D}: \theta_i) = \prod_{m} P(x[m]|\pmb{u}_[m] : \theta) = \prod_{m} P(x[m]|\pmb{u}_[m] : \theta_{X|\pmb{U}})](https://s0.wp.com/latex.php?latex=L_i%28%7B%5Ccal+D%7D%3A+%5Ctheta_i%29+%3D+%5Cprod_%7Bm%7D+P%28x%5Bm%5D%7C%5Cpmb%7Bu%7D_%5Bm%5D+%3A+%5Ctheta%29+%3D+%5Cprod_%7Bm%7D+P%28x%5Bm%5D%7C%5Cpmb%7Bu%7D_%5Bm%5D+%3A+%5Ctheta_%7BX%7C%5Cpmb%7BU%7D%7D%29&bg=ffffff&fg=333333&s=0&c=20201002)
Re-arranjando os produtos para agrupá-los por valores de  e
e  (buckets), temos
(buckets), temos
![\displaystyle = \prod_{x, \pmb{u}} \prod_{\substack{m:x[m] = x\\\pmb{u}[m] = \pmb{u}}} P(x[m]|\pmb{u}_[m] : \theta_{X|\pmb{U}})](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%3D+%5Cprod_%7Bx%2C+%5Cpmb%7Bu%7D%7D+%5Cprod_%7B%5Csubstack%7Bm%3Ax%5Bm%5D+%3D+x%5C%5C%5Cpmb%7Bu%7D%5Bm%5D+%3D+%5Cpmb%7Bu%7D%7D%7D+P%28x%5Bm%5D%7C%5Cpmb%7Bu%7D_%5Bm%5D+%3A+%5Ctheta_%7BX%7C%5Cpmb%7BU%7D%7D%29&bg=ffffff&fg=333333&s=0&c=20201002)
Observamos que  corresponde a uma entrada do CPD dado por
corresponde a uma entrada do CPD dado por  , que denotamos por
, que denotamos por  , portanto,
, portanto,
![\displaystyle = \prod_{x, \pmb{u}} \prod_{\substack{m:x[m] = x\\\pmb{u}[m] = \pmb{u}}} \theta_{x|\pmb{u}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%3D+%5Cprod_%7Bx%2C+%5Cpmb%7Bu%7D%7D+%5Cprod_%7B%5Csubstack%7Bm%3Ax%5Bm%5D+%3D+x%5C%5C%5Cpmb%7Bu%7D%5Bm%5D+%3D+%5Cpmb%7Bu%7D%7D%7D+%5Ctheta_%7Bx%7C%5Cpmb%7Bu%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Note que o termo  será multiplicado pelo número de amostras tais que
será multiplicado pelo número de amostras tais que ![x[m] = x](https://s0.wp.com/latex.php?latex=x%5Bm%5D+%3D+x&bg=ffffff&fg=333333&s=0&c=20201002) e
e ![\pmb{u}[m] = \pmb{u}](https://s0.wp.com/latex.php?latex=%5Cpmb%7Bu%7D%5Bm%5D+%3D+%5Cpmb%7Bu%7D&bg=ffffff&fg=333333&s=0&c=20201002) , que denotamos por
, que denotamos por ![M[x,\pmb{u}]](https://s0.wp.com/latex.php?latex=M%5Bx%2C%5Cpmb%7Bu%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
,
![\displaystyle = \prod_{x, \pmb{u}} \theta_{x|\pmb{u}}^{M[x,\pmb{u}]}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%3D+%5Cprod_%7Bx%2C+%5Cpmb%7Bu%7D%7D+%5Ctheta_%7Bx%7C%5Cpmb%7Bu%7D%7D%5E%7BM%5Bx%2C%5Cpmb%7Bu%7D%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Finalmente, vemos que a distribuição  corresponde à distribuição multinomial, então podemos calcular o MLE
corresponde à distribuição multinomial, então podemos calcular o MLE  como
como
![\theta^*_{x|\pmb{u}} = \dfrac{M[x,\pmb{u}]}{\sum_{x'} M[x',\pmb{u}]} = \dfrac{M[x,\pmb{u}]}{M[\pmb{u}]}](https://s0.wp.com/latex.php?latex=%5Ctheta%5E%2A_%7Bx%7C%5Cpmb%7Bu%7D%7D+%3D+%5Cdfrac%7BM%5Bx%2C%5Cpmb%7Bu%7D%5D%7D%7B%5Csum_%7Bx%27%7D+M%5Bx%27%2C%5Cpmb%7Bu%7D%5D%7D+%3D+%5Cdfrac%7BM%5Bx%2C%5Cpmb%7Bu%7D%5D%7D%7BM%5B%5Cpmb%7Bu%7D%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
CPDs compartilhados. Note que a fórmula que obtivemos depende apenas dos valores de  e
e  e do CPD
e do CPD  . Assim, se tivermos CPDs compartilhados entre variáveis, como no modelo temporal, a única diferença é que podemos contar as ocorrências em
. Assim, se tivermos CPDs compartilhados entre variáveis, como no modelo temporal, a única diferença é que podemos contar as ocorrências em ![M[x,\pmb{u}]](https://s0.wp.com/latex.php?latex=M%5Bx%2C%5Cpmb%7Bu%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) múltiplas vezes para uma mesma amostra.
múltiplas vezes para uma mesma amostra.
Observamos finalmente que o número de buckets cresce exponencialmente com o número de pais da variável. Isso faz com que os valores de ![\frac{M[x,\pmb{u}]}{M[\pmb{u}]}](https://s0.wp.com/latex.php?latex=%5Cfrac%7BM%5Bx%2C%5Cpmb%7Bu%7D%5D%7D%7BM%5B%5Cpmb%7Bu%7D%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) fiquem muito pequenos, levando à ocorrência da fragmentação e requerendo um maior número de amostras.
fiquem muito pequenos, levando à ocorrência da fragmentação e requerendo um maior número de amostras.
Estimativa Bayesiana
Uma maneira alternativa de se fazer estimativas das distribuições dos CPDs é usando uma outra rede Bayesiana. Neste caso supomos que cada amostra de  representa um nó da rede e elas dependem de uma variável contínua que representa a distribuição
representa um nó da rede e elas dependem de uma variável contínua que representa a distribuição 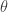 .
.
Neste caso a variável 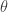 tem um CPD correspondente a uma distribuição inicial
tem um CPD correspondente a uma distribuição inicial  . A ideia é usar a rede para determinar a distribuição a posteriori de
. A ideia é usar a rede para determinar a distribuição a posteriori de  uma vez que observamos
uma vez que observamos  . Usando a regra de Bayes temos que,
. Usando a regra de Bayes temos que,
(1) ![P(\theta|x[1], \cdots, x[M]) = \dfrac{P(x[1], \cdots, x[M]|\theta) P(\theta)}{P(x[1], \cdots, x[M])}](https://s0.wp.com/latex.php?latex=P%28%5Ctheta%7Cx%5B1%5D%2C+%5Ccdots%2C+x%5BM%5D%29+%3D+%5Cdfrac%7BP%28x%5B1%5D%2C+%5Ccdots%2C+x%5BM%5D%7C%5Ctheta%29+P%28%5Ctheta%29%7D%7BP%28x%5B1%5D%2C+%5Ccdots%2C+x%5BM%5D%29%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Veja que o primeiro termo do numerador corresponde à verossimilhança.  é a distribuição a priori e
é a distribuição a priori e ![P(\theta|x[1], \cdots, x[M])](https://s0.wp.com/latex.php?latex=P%28%5Ctheta%7Cx%5B1%5D%2C+%5Ccdots%2C+x%5BM%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) a distribuição a posteriori. Uma vez que temos o conjunto de amostragem, o denominador é uma constante normalizadora.
a distribuição a posteriori. Uma vez que temos o conjunto de amostragem, o denominador é uma constante normalizadora.
Portanto, podemos reescrever (1) como
(2) 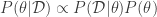
Distribuição multinomial
Suponha que 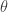 é uma distribuição multinomial sobre
é uma distribuição multinomial sobre 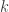 valores. Como um valor a priori da distribuição de
valores. Como um valor a priori da distribuição de 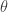 , em geral utiliza-se a distribuição de Dirichlet, denotada por
, em geral utiliza-se a distribuição de Dirichlet, denotada por  , onde
, onde 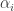 é chamado de hiper-parâmetro. Basicamente, a distribuição é proporcional a um produtório,
é chamado de hiper-parâmetro. Basicamente, a distribuição é proporcional a um produtório,

Intuitivamente os hiper-parâmetros correspondem às frequências de variáveis amostradas discriminadas por valor.
Usando a distribuição de Dirichlet como a distribuição a priori e lembrando que para uma distribuição multinomial a verossimilhança é dada por

Por (2), concluímos que a distribuição a posteriori é dada por,
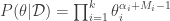
Note que  , ou seja, a distribuição a posteriori continuou sendo uma distribuição de Dirichlet. Devido a essa característica, dizemos que a distribuição de Dirichlet é um conjugado a priori para a distribuição multinomial.
, ou seja, a distribuição a posteriori continuou sendo uma distribuição de Dirichlet. Devido a essa característica, dizemos que a distribuição de Dirichlet é um conjugado a priori para a distribuição multinomial.
Previsão Bayesiana
Considere uma rede bayesiana simples como a da Figura 1. Suponha que a variável 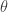 tem distribuição
tem distribuição  .
.

Figura 1: Variável condicionada por uma distribuição de Dirichlet
Podemos calcular a distribuição em 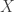 multiplicando os CPD’s e marginalizando
multiplicando os CPD’s e marginalizando 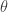 , ou seja,
, ou seja,
(3) 
Para um valor específico de  , temos que
, temos que  . Substituindo também
. Substituindo também  pela definição da eq. de Dirichlet teremos
pela definição da eq. de Dirichlet teremos
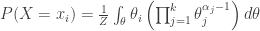
Que segundo as aulas é igual a
(4) 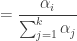
Agora, suponha que tenhamos um conjunto de 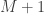 variáveis condicionadas por
variáveis condicionadas por 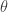 , que novamente supomos possuir a distribuição
, que novamente supomos possuir a distribuição  , conforme a Figura 2.
, conforme a Figura 2.

Figura 2: Rede Bayesiana com M+1 variáveis condicionadas a uma distribuição de Dirichlet
Imagine que observamos as 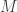 primeiras variáveis (conjunto
primeiras variáveis (conjunto  ) e queremos prever a distribuição da
) e queremos prever a distribuição da 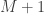 -ésima, temos que
-ésima, temos que
![P(X[M+1] | {\cal D}) = \int_{\theta} P(X[M+1]|{\cal D},\theta) P(\theta|{\cal D}) d\theta](https://s0.wp.com/latex.php?latex=P%28X%5BM%2B1%5D+%7C+%7B%5Ccal+D%7D%29+%3D+%5Cint_%7B%5Ctheta%7D+P%28X%5BM%2B1%5D%7C%7B%5Ccal+D%7D%2C%5Ctheta%29+P%28%5Ctheta%7C%7B%5Ccal+D%7D%29+d%5Ctheta&bg=ffffff&fg=333333&s=0&c=20201002)
Dado 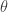 ,
, ![X[M+1]](https://s0.wp.com/latex.php?latex=X%5BM%2B1%5D&bg=ffffff&fg=333333&s=0&c=20201002) é independente de
é independente de  , logo
, logo
![P(X[M+1] | {\cal D}) = \int_{\theta} P(X[M+1]|\theta) P(\theta|{\cal D}) d\theta](https://s0.wp.com/latex.php?latex=P%28X%5BM%2B1%5D+%7C+%7B%5Ccal+D%7D%29+%3D+%5Cint_%7B%5Ctheta%7D+P%28X%5BM%2B1%5D%7C%5Ctheta%29+P%28%5Ctheta%7C%7B%5Ccal+D%7D%29+d%5Ctheta&bg=ffffff&fg=333333&s=0&c=20201002)
Vimos anteriormente que  . Note então que o lado direito da equação acima é idêntico ao lado direito da equação (3). Portanto, podemos calcular $P(X[M+1] = x_i |{\cal D})$, mas usando
. Note então que o lado direito da equação acima é idêntico ao lado direito da equação (3). Portanto, podemos calcular $P(X[M+1] = x_i |{\cal D})$, mas usando  , levando a
, levando a
(5) ![P(X[M+1] = x_i |{\cal D}) = \dfrac{\alpha_i + M_i}{\sum_{j=1}^{k} (\alpha_j + M_j)}](https://s0.wp.com/latex.php?latex=P%28X%5BM%2B1%5D+%3D+x_i+%7C%7B%5Ccal+D%7D%29+%3D+%5Cdfrac%7B%5Calpha_i+%2B+M_i%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bk%7D+%28%5Calpha_j+%2B+M_j%29%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Definimos como o tamanho da amostra equivalente a soma 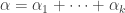 . Observe que se
. Observe que se  , teríamos o MLE.
, teríamos o MLE.
Usando redes Bayesianas, damos um “chute” inicial na distribuição, que eventualmente converge para o mesmo valor que o MLE conforme o número de iterações aumenta. A vantagem é que temos uma maior robustez nas iterações iniciais, quando temos poucas amostras. O gráfico da Figura 3 mostra bem esse fenômeno.

Figura 3: Gráfico de estimativa de uma distribuição de Bernoulli, usando diferentes métodos.
Note que a magnitude de 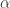 define o quanto a distribuição inicial terá efeito sobre as distribuições obtidas a priori. Veja como a Dir(.5,.5) (verde-claro) quase não tem diferença sobre a MLE, enquanto Dir(10,10) (preto) muda bastante.
define o quanto a distribuição inicial terá efeito sobre as distribuições obtidas a priori. Veja como a Dir(.5,.5) (verde-claro) quase não tem diferença sobre a MLE, enquanto Dir(10,10) (preto) muda bastante.
Estimativas Bayesianas para Redes Bayesianas
Podemos generalizar as ideias apresentadas anteriormente para estimar as distribuições dos CPDs de toda uma rede Bayesiana. Consideremos uma rede Bayesiana com uma variável 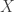 e uma variável
e uma variável 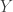 que depende condicionalmente de
que depende condicionalmente de 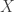 .
.
Para estimar os CPDs dessas duas variáveis usando um conjunto de 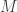 amostras, podemos construir outra rede Bayesiana conforme a Figura 4.
amostras, podemos construir outra rede Bayesiana conforme a Figura 4.

Figura 4: Estimativa de parâmetros para uma rede Bayesiana”
Note que 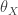 corresponde ao CPD de
corresponde ao CPD de 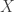 e
e  corresponde ao CPD de
corresponde ao CPD de 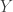 . Se partirmos de distribuições iniciais para
. Se partirmos de distribuições iniciais para 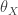 e
e  , temos que as amostras
, temos que as amostras ![(X[m], Y[m])](https://s0.wp.com/latex.php?latex=%28X%5Bm%5D%2C+Y%5Bm%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) são independentes.
são independentes.
Dado o conjunto de amostras 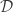 , temos que
, temos que 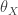 e
e  são independentes. Assim, a distribuição a posteriori de
são independentes. Assim, a distribuição a posteriori de 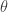 pode ser dada por
pode ser dada por

Podemos refinar o modelo e considerar os possíveis valores de 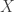 , criando um CPD de
, criando um CPD de 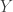 para cada valor. Por exemplo, se
para cada valor. Por exemplo, se 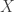 for uma variável binária teremos a rede Bayesiana da Figura 5
for uma variável binária teremos a rede Bayesiana da Figura 5

Figura 5: Estimativa refinada de parâmetros para uma rede Bayesiana
Neste caso, dado o conjunto  , não fica evidente pela rede que
, não fica evidente pela rede que 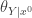 é independente de
é independente de  , mas aqui temos independência específica por contexto, pois quando o valor de
, mas aqui temos independência específica por contexto, pois quando o valor de 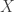 é conhecido, uma das duas arestas incidentes a cada
é conhecido, uma das duas arestas incidentes a cada ![Y[m]](https://s0.wp.com/latex.php?latex=Y%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) some.
some.
De qualquer maneira, podemos computar as probabilidades a posteriori de 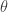 independentemente. Se a distribuição a priori de
independentemente. Se a distribuição a priori de  for
for  , a distribuição a posteriori será
, a distribuição a posteriori será ![Dir(\alpha_{x^1|\pmb{u}} + M[x^1|\pmb{u}], \cdots, \alpha_{x^k|\pmb{u}} + M[x^k|\pmb{u}])](https://s0.wp.com/latex.php?latex=Dir%28%5Calpha_%7Bx%5E1%7C%5Cpmb%7Bu%7D%7D+%2B+M%5Bx%5E1%7C%5Cpmb%7Bu%7D%5D%2C+%5Ccdots%2C+%5Calpha_%7Bx%5Ek%7C%5Cpmb%7Bu%7D%7D+%2B+M%5Bx%5Ek%7C%5Cpmb%7Bu%7D%5D%29&bg=ffffff&fg=333333&s=0&c=20201002)
Uma escolha inicial dos hiper-parâmetros das distribuições de Dirichlet, consiste em escolher um tamanho de amostra equivalente 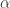 e para cada CPD distribuí-lo pelo número de entradas. Por exemplo, se o CPD for sobre uma única variável binária, teremos
e para cada CPD distribuí-lo pelo número de entradas. Por exemplo, se o CPD for sobre uma única variável binária, teremos  . Se tivermos uma variável binária dependendo de outra, fazemos a divisão de
. Se tivermos uma variável binária dependendo de outra, fazemos a divisão de 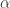 por 4.
por 4.
Estimativa de parâmetros em Redes de Markov
Vamos apresentar métodos para a estimativa de parâmetros em redes de Markov ou MRF (Markov Random Fields) e para redes de Markov condicionais ou CRF (Conditional Random Fields). Ao invés de um produto de fatores, vamos considerar a representação mais genéricas através de modelos log-lineares.
Verossimilhança máxima para modelos log-lineares
Considere uma distribuição conjunta de um modelo log-linear
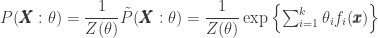
Note que para simplificar a notação, estamos supondo que 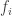 ignora todas as entradas de
ignora todas as entradas de  que não pertencem a seu domínimo
que não pertencem a seu domínimo 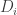 . Aqui
. Aqui  é a constante normalizadora dada pela soma de
é a constante normalizadora dada pela soma de  para todos as possíveis atribuições
para todos as possíveis atribuições  , ou seja
, ou seja

Podemos definir a log-verossimilhança de um conjunto de amostras  , denotado por
, denotado por  como
como
![\ell(\theta:{\cal D}) = \ln (L(\theta:{\cal D})) = \sum_m(\ln P(\pmb{x}[m] : \theta))](https://s0.wp.com/latex.php?latex=%5Cell%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D+%5Cln+%28L%28%5Ctheta%3A%7B%5Ccal+D%7D%29%29+%3D+%5Csum_m%28%5Cln+P%28%5Cpmb%7Bx%7D%5Bm%5D+%3A+%5Ctheta%29%29&bg=ffffff&fg=333333&s=0&c=20201002)
Substituindo ![P(\pmb{x}[m] : \theta)](https://s0.wp.com/latex.php?latex=P%28%5Cpmb%7Bx%7D%5Bm%5D+%3A+%5Ctheta%29&bg=ffffff&fg=333333&s=0&c=20201002) pela distribuição log-linear temos
pela distribuição log-linear temos
![= \sum_m (\sum_i \theta_i f_i(\pmb{x}[m]) - \ln Z(\theta))](https://s0.wp.com/latex.php?latex=%3D+%5Csum_m+%28%5Csum_i+%5Ctheta_i+f_i%28%5Cpmb%7Bx%7D%5Bm%5D%29+-+%5Cln+Z%28%5Ctheta%29%29&bg=ffffff&fg=333333&s=0&c=20201002)
podemos re-arrajar os somatórios e obter:
![= (\sum_i \theta_i (\sum_m f_i(\pmb{x}[m]))) - M\ln Z(\theta)](https://s0.wp.com/latex.php?latex=%3D+%28%5Csum_i+%5Ctheta_i+%28%5Csum_m+f_i%28%5Cpmb%7Bx%7D%5Bm%5D%29%29%29+-+M%5Cln+Z%28%5Ctheta%29&bg=ffffff&fg=333333&s=0&c=20201002)
Diferentemente do caso de redes Bayesianas, aqui não podemos decompor em verossimilhanças locais porque o termo  acopla os termos
acopla os termos  .
.
Porém, podemos mostrar que essa função é côncava, podendo ser resolvida numericamente por um método de descida de gradiente, por exemplo. Na prática, costuma-se utilizar o L-BFGS (Low Memory Broyden Fletcher Goldfarb Shanno).
Para computar os gradientes, vamos considerar a derivada da log-verossimilhança.
![\dfrac{\partial}{\partial\theta_i} \dfrac{1}{M} \ell(\theta:{\cal D}) = \dfrac{\partial}{\partial\theta_i} \left((\sum_i \theta_i \dfrac{1}{M} (\sum_m f_i(\pmb{x}[m]))) - \ln Z(\theta)\right)](https://s0.wp.com/latex.php?latex=%5Cdfrac%7B%5Cpartial%7D%7B%5Cpartial%5Ctheta_i%7D+%5Cdfrac%7B1%7D%7BM%7D+%5Cell%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D++%5Cdfrac%7B%5Cpartial%7D%7B%5Cpartial%5Ctheta_i%7D+%5Cleft%28%28%5Csum_i+%5Ctheta_i+%5Cdfrac%7B1%7D%7BM%7D+%28%5Csum_m+f_i%28%5Cpmb%7Bx%7D%5Bm%5D%29%29%29+-+%5Cln+Z%28%5Ctheta%29%5Cright%29&bg=ffffff&fg=333333&s=0&c=20201002)
Note que dividimos a log-verossimilhança pela constante 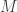 antes de derivar. Isso é para simplificar o resultado. Como estamos derivando com relacão a
antes de derivar. Isso é para simplificar o resultado. Como estamos derivando com relacão a 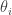 , o único termo que restará do primeiro somatório é
, o único termo que restará do primeiro somatório é
![\dfrac{1}{M} \sum_m f_i(x[m])](https://s0.wp.com/latex.php?latex=%5Cdfrac%7B1%7D%7BM%7D+%5Csum_m+f_i%28x%5Bm%5D%29&bg=ffffff&fg=333333&s=0&c=20201002)
que corresponde à média dos valores de 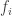 considerando todas as amostras. Definimos esse termo como esperança empírica, denotada por
considerando todas as amostras. Definimos esse termo como esperança empírica, denotada por ![E_{\cal D}[f_i(\pmb{X})]](https://s0.wp.com/latex.php?latex=E_%7B%5Ccal+D%7D%5Bf_i%28%5Cpmb%7BX%7D%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Veja que este valor independe da distribuição
. Veja que este valor independe da distribuição 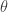 .
.
Já para o segundo termo, aplicamos inicialmente a regra da cadeia para obter

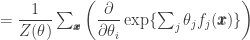
Podemos aplicar novamente a regra da cadeia para  , obtendo
, obtendo

Rearranjando os termos ficamos com

Veja que o priimeiro termo do somatório é exatamente nossa distribuição original,  com
com 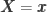 . Reescrevendo temos:
. Reescrevendo temos:

Esse termo representa a esperança de 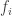 considerando a distribuição
considerando a distribuição 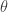 e será denotado por
e será denotado por ![E_\theta[f_i]](https://s0.wp.com/latex.php?latex=E_%5Ctheta%5Bf_i%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Veja que para calcular a probabilidade de cada possível atribuição
. Veja que para calcular a probabilidade de cada possível atribuição  , podemos usar os métodos de inferência vistos em aulas passadas.
, podemos usar os métodos de inferência vistos em aulas passadas.
Resumindo, temos o seguinte resultado:
![\dfrac{\partial}{\partial\theta_i} \dfrac{1}{M} \ell(\theta:{\cal D}) = E_{\cal D}[f_i(\pmb{X})] - E_\theta[f_i]](https://s0.wp.com/latex.php?latex=%5Cdfrac%7B%5Cpartial%7D%7B%5Cpartial%5Ctheta_i%7D+%5Cdfrac%7B1%7D%7BM%7D+%5Cell%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D+E_%7B%5Ccal+D%7D%5Bf_i%28%5Cpmb%7BX%7D%29%5D+-+E_%5Ctheta%5Bf_i%5D&bg=ffffff&fg=333333&s=0&c=20201002)
Usando essa diferença para construir o gradiente, obtemos finalmente o seguinte teorema:
Teorema. A distribuição  resulta na MLE se e somente se
resulta na MLE se e somente se ![E_{\cal D}[f_i(X)] = E_\theta[f_i]](https://s0.wp.com/latex.php?latex=E_%7B%5Ccal+D%7D%5Bf_i%28X%29%5D+%3D+E_%5Ctheta%5Bf_i%5D&bg=ffffff&fg=333333&s=0&c=20201002) para todo
para todo 
MLE para CRFs
No caso de CRFs (Conditional Random Fields), temos a distribuição conjunta condicional
 ,
,
onde 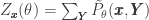
Considere o conjunto de amostras ![{\cal D} = \{(x[m], y[m])\}_{m=1}^M](https://s0.wp.com/latex.php?latex=%7B%5Ccal+D%7D+%3D+%5C%7B%28x%5Bm%5D%2C+y%5Bm%5D%29%5C%7D_%7Bm%3D1%7D%5EM&bg=ffffff&fg=333333&s=0&c=20201002) . Podemos novamente definir a log-verossimilhança:
. Podemos novamente definir a log-verossimilhança:
![\ell_{Y|x}(\theta:{\cal D}) = \sum_{m=1}^M \ln P_\theta(y[m], x[m] : \theta)](https://s0.wp.com/latex.php?latex=%5Cell_%7BY%7Cx%7D%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D+%5Csum_%7Bm%3D1%7D%5EM+%5Cln+P_%5Ctheta%28y%5Bm%5D%2C+x%5Bm%5D+%3A+%5Ctheta%29&bg=ffffff&fg=333333&s=0&c=20201002)
![= \sum_m (\sum_i \theta_i f_i(\pmb{x}[m]) - \ln Z_{x[m]}(\theta))](https://s0.wp.com/latex.php?latex=%3D+%5Csum_m+%28%5Csum_i+%5Ctheta_i+f_i%28%5Cpmb%7Bx%7D%5Bm%5D%29+-+%5Cln+Z_%7Bx%5Bm%5D%7D%28%5Ctheta%29%29&bg=ffffff&fg=333333&s=0&c=20201002)
Note que neste caso não podemos extrair o termo ![Z_{x[m]}(\theta)](https://s0.wp.com/latex.php?latex=Z_%7Bx%5Bm%5D%7D%28%5Ctheta%29&bg=ffffff&fg=333333&s=0&c=20201002) para fora do somatório porque ele depende de
para fora do somatório porque ele depende de ![x[m]](https://s0.wp.com/latex.php?latex=x%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Para determinar o gradiente, podemos novamente calcular a derivada em relação a 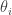 :
:
![\dfrac{\partial}{\partial \theta_i} \dfrac{1}{M} \ell_{Y|x}(\theta:{\cal D}) = \dfrac{\partial}{\partial \theta_i} \dfrac{1}{M} \sum_m (\sum_i \theta_i f_i(\pmb{x}[m]) - \ln Z_{x[m]}(\theta))](https://s0.wp.com/latex.php?latex=%5Cdfrac%7B%5Cpartial%7D%7B%5Cpartial+%5Ctheta_i%7D+%5Cdfrac%7B1%7D%7BM%7D+%5Cell_%7BY%7Cx%7D%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D+%5Cdfrac%7B%5Cpartial%7D%7B%5Cpartial+%5Ctheta_i%7D+%5Cdfrac%7B1%7D%7BM%7D+%5Csum_m+%28%5Csum_i+%5Ctheta_i+f_i%28%5Cpmb%7Bx%7D%5Bm%5D%29+-+%5Cln+Z_%7Bx%5Bm%5D%7D%28%5Ctheta%29%29&bg=ffffff&fg=333333&s=0&c=20201002)
Usando as mesmas ideias do caso de MRF’s, concluiremos que
![\dfrac{\partial}{\partial \theta_i} \dfrac{1}{M} \ell_{Y|X}(\theta:{\cal D}) = \dfrac{1}{M} \sum_{m=1}^{M} (f_i(x[m],y[m]) - E_\theta[f_i(x[m], Y)])](https://s0.wp.com/latex.php?latex=%5Cdfrac%7B%5Cpartial%7D%7B%5Cpartial+%5Ctheta_i%7D+%5Cdfrac%7B1%7D%7BM%7D+%5Cell_%7BY%7CX%7D%28%5Ctheta%3A%7B%5Ccal+D%7D%29+%3D+%5Cdfrac%7B1%7D%7BM%7D+%5Csum_%7Bm%3D1%7D%5E%7BM%7D+%28f_i%28x%5Bm%5D%2Cy%5Bm%5D%29+-+E_%5Ctheta%5Bf_i%28x%5Bm%5D%2C+Y%29%5D%29&bg=ffffff&fg=333333&s=0&c=20201002)
Onde ![E_\theta[f_i(x[m], Y)] = \sum_Y P_\theta(Y|x[m]) f_j(Y, x[m])](https://s0.wp.com/latex.php?latex=E_%5Ctheta%5Bf_i%28x%5Bm%5D%2C+Y%29%5D+%3D++%5Csum_Y+P_%5Ctheta%28Y%7Cx%5Bm%5D%29+f_j%28Y%2C+x%5Bm%5D%29&bg=ffffff&fg=333333&s=0&c=20201002)
A diferença aqui é que a cada passo do algoritmo, devemos recalcular ![P_\theta(Y|x[m])]](https://s0.wp.com/latex.php?latex=P_%5Ctheta%28Y%7Cx%5Bm%5D%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) para cada amostra
para cada amostra ![x[m]](https://s0.wp.com/latex.php?latex=x%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Porém, em geral o conjunto
. Porém, em geral o conjunto 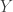 será menor para CRF’s.
será menor para CRF’s.
Estimativa MAP para MRFs e CRFs
Da mesma forma que para redes Bayesianas, podemos “chutar” uma distribuição a priori e obter uma distribuição a posteriori. Entretanto, devido ao acoplamento presente na verossimilhança de redes de Markov, não há uma fórmula fechada para a distribuição, como a de Dirichlet para redes Bayesianas.
O que fazemos é manter um conjunto de parâmetros que maximizem a dstribuição a posteriori, ou seja, uma MAP (Maximum A Posteriori).
Uma possível distribuição a pirori que pode ser usada é a distribuição gaussiana com métia 0.

Intuitivamente, quanto maior o valor de 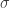 , maior a confiança de que o valor de
, maior a confiança de que o valor de  esteja próximo de 0.
esteja próximo de 0.
Outra alternativa é usar a distribuição de Laplace,

Queremos encontrar a distribuição  que maximiza a distribuição conjunta dado o conjunto de amostras, ou seja,
que maximiza a distribuição conjunta dado o conjunto de amostras, ou seja,

Neste caso  é a verossimilhança e
é a verossimilhança e  é a distribuição a priori. Como o logaritmo é monotomicamente crescente com sua entrada, podemos aplicar o log ao termo dentro de argmax:
é a distribuição a priori. Como o logaritmo é monotomicamente crescente com sua entrada, podemos aplicar o log ao termo dentro de argmax:

O plot de  para a distribuição Gaussiana, é uma função quadrática. Esta curva corresponde a uma penalização da log-verossimilhança e é conhecida como regularização-L2.
para a distribuição Gaussiana, é uma função quadrática. Esta curva corresponde a uma penalização da log-verossimilhança e é conhecida como regularização-L2.
De maneira análoga, o plot para a distribuição de Laplace é uma função linear e é equivalente à regularização-L1.
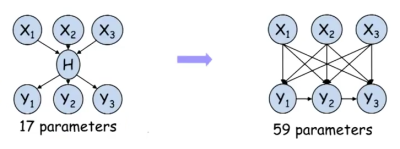
reduz o número de arestas no modelo e consequentemente o número de parâmetros.
representa o parâmetro para a atribuição
e
no CPD de
. Temos que
representa a probabilidade da atribuição
e
dadas as amostras e os parâmetros
.
. Usando inferência em uma árvore-clique apenas uma vez para um dado
, conseguimos obter
.
calcule
para todas as atribuições de
. Compute as estatísticas suficientes esperadas ou ESS (Expected Sufficient Statistics) para cada atribuição
, dadas por
(
) o conjunto de variáveis de
(
) que estão faltando em
. Podemos concluir que
melhora a cada iteração nesse método.




 Publicado por kunigami
Publicado por kunigami 




 Feed dos posts
Feed dos posts
Deverá estar ligado para publicar um comentário.